-- Da waere meine Antwort. F x3ax22bxc f x 3ax2 2bxc.
Ganzrationale Funktion 3. Grades - Spaß für meinen eigenen Blog, bei dieser Gelegenheit werde ich Ihnen im Zusammenhang mit erklären Ganzrationale Funktion 3. Grades. Also, wenn Sie großartige Aufnahmen machen möchten Ganzrationale Funktion 3. Grades, Klicken Sie einfach auf das Speichersymbol, um das Foto auf Ihrem Computer zu speichern. Sie können heruntergeladen werden. Wenn Sie möchten und möchten, klicken Sie im Beitrag auf "Logo speichern". Der Download erfolgt direkt auf Ihren Heimcomputer.
Ganzrationale Funktion 3. Grades ist eine wichtige Information, die von Fotos und HD-Bildern begleitet wird, die von allen Websites der Welt stammen. Laden Sie dieses Bild kostenlos in High Definition-Auflösung mit der unten stehenden Option "Download-Schaltfläche" herunter. Wenn Sie nicht die genaue Auflösung finden, nach der Sie suchen, wählen Sie Original oder eine höhere Auflösung. Sie können diese Seite auch einfach speichern, sodass Sie sie jederzeit anzeigen können.
Vielen Dank für Ihren Besuch unserer Website, Artikel oben, veröffentlicht von Babang Tampan. Hoffe du mag bleibe genau hier. Für viele Upgrades und Aktuelle Informationen zum folgenden Foto folgen Sie uns bitte auf Twitter, Pfad, Instagram, oder Sie markieren diese Seite auf Lesezeichen Abschnitt, Wir versuchen Ihnen up grade regelmäßig mit alles neu und frisch Bilder, genieße dein Surfen und finde das Beste für dich. Heute Wir sind aufgeregt, zu erklären dass wir entdeckt haben ein unglaublich interessanter Inhalt, der besprochen, viele Individuen suchen Informationen über zu finden, und sicher einer von diesen bist du, nicht wahr?
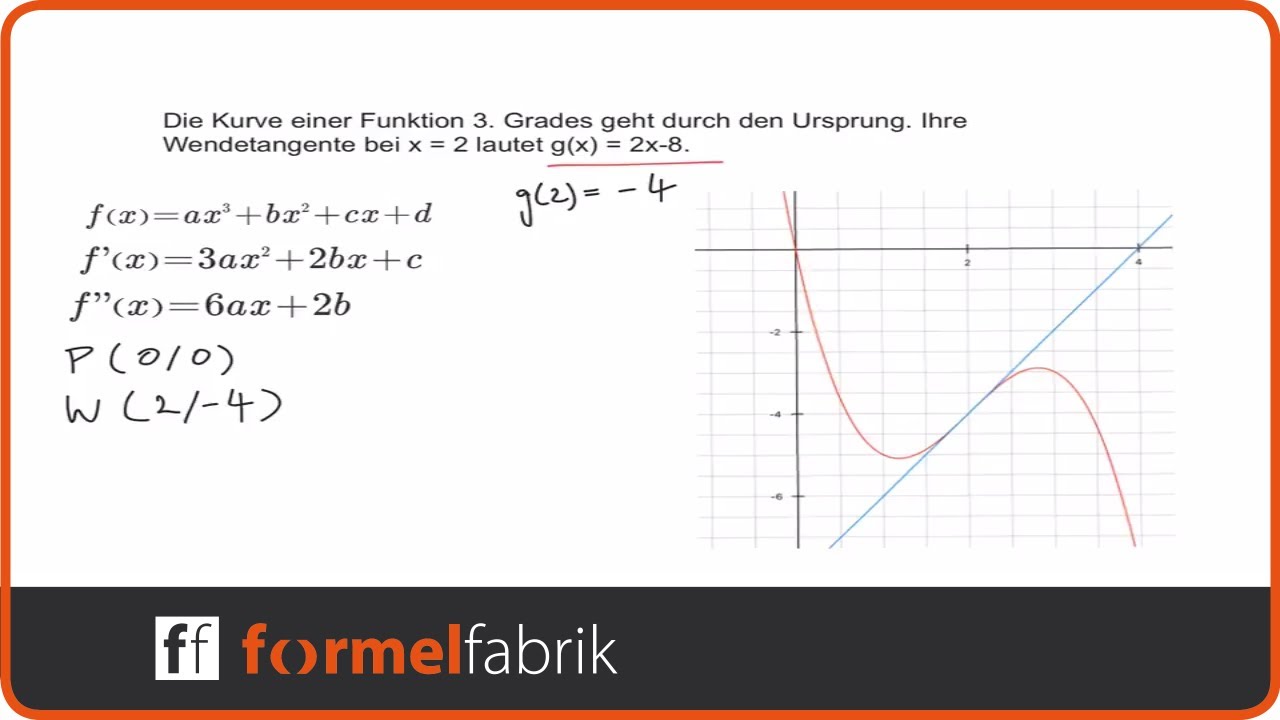 Steckbriefaufgabe Funktion 3 Grades Mit Wendetangente Youtube
Steckbriefaufgabe Funktion 3 Grades Mit Wendetangente Youtube
Produktionsmenge x in ME.
Ganzrationale funktion 3. grades. F x6ax2b f x 6ax2b. F x 3 a x 2 2 b x c. Fuer eine ganzrationale Funktion dritten grades gilt.
Fx2x 3-4x 2 3x-1. A 0 6. Die Umgehungsstrasse muende bei A tangential in die Ortsdurchfahrt und treffe im Punkt C auf die vorhandene Ortsdurchfahrt unter einem beliebigen Winkel.
Grades sieben Nullstellen haben koennte. F x a x 3 b x 2 c x d. Wie man dabei vorgeht und auf was man besonders achten muss wird in d.
Durch den Ort G verlaufe eine geradlinig verlaufende Ortsdurchfahrt durch die Punkte A -23 und C 2-1. Allgemein hat eine ganzrationale Funktion dritten Grades diese Form. B Der Graph einer ganzrationalen Funktion dritten Grades hat im Ursprung und im Punkt P24 jeweils ein Extremum.
A 1 2. Bestimmen Sie die Gewinnzone und den maximalen Gewinn wenn der Verkaufspreis je ME. Bestimmen Sie den Funktionsterm aus der Tabelle.
Ist eine konstante Funktion. Aufgaben Extrempunkte ganzr Funktion dritten Grades Trainingsaufgaben Extrempunkte ganzrationaler Funktionen dritten Grades Untersuchen Sie die folgenden ganzrationalen Funktionen auf Extremwerte und bestimmen Sie gegebenenfalls die Extrempunkte. Grades soll anhand bestimmter Vorgaben gefunden werden.
Loesung zu Aufgabe 2 Nach dem Satz vom Nullprodukt gilt dass die Gleichung der Funktion mindestens aus den Faktoren besteht da beides Nullstellen sind. Ist eine lineare Funktion. Begruende dass es keine ganzrationale Funktion 3.
F x 6 a x 2 b. A 2 4. Grades wird kubische Funktion genannt.
Grades mit den Extremstellen x2 und x5 und der Wendestelle x3 gibt. X R und abcd R a ungleich 0. X 2 x x 1 x 3 2 displaystyle fcolon xmapsto -2xx-1x32 muss der Funktionsterm zunaechst durch Aufloesen der Klammern in eine Summe umgeschrieben werden.
Markieren Sie den Wendepunkt rot. Die Funktion f hat vier Nullstellen und zwar x 1 4 x 2 1 x 3 1 x 4 3 obwohl eine ganzrationale Funktion 7. Hier lassen sich die wichtigsten Punkte wie folgt zusammenfassen.
Grades ist eine Parabel weshalb es entweder ein lokales Maximum oder ein lokales Minimum nur geben kann. F xax3bx2cxd f x ax3 bx2cxd. Eine ganzrationale Funktion 3.
Gib ohne Rechnung eine ganzrationale Funktion dritten Grades an die eine einfache Nullstelle bei und eine zweifache Nullstelle bei hat. Setze dies ein du erhaeltst Gleichungen mit 3 Unbekannten abc. Fxax3bx2cx W24 Wendepunkt--- f24.
Die Funktion mit dem Term ist eine ganzrationale Funktion vom Grad 3 mit den Koeffizienten und. Student Braucht man dafuer nicht ein hoch und tiefpunkt. A 0 3.
Bestimmen Sie die ganzrationale Funktion 4. 0 2 Hausaufgaben-Loesungen von Experten. Ganzrationale Funktion dritten Grades.
Bestimme die Gleichung einer ganzrationalen funktion dritten grades deren graph punktsymmetrisch zum Ursprung ist und in H35 einen hochpunkt hat. Die erste Aussage dazu lautet F ist eine ganzrationale Funktion vierten Grades hat als Nullstellen 2 und -3 und sonst keine weitere Nullstellen. Zeichnen Sie das Schaubild von K.
Ziel ist es deren Grad und die Koeffizienten zu bestimmen. A Die Funktion ist vom Grad 4 und besitzt genau ein lokales Maximum und ein lokales Minimum. Fxa 3 x 3 a 2 x 2 a 1 xa 0.
Wendetangente hat Steigung -3. A 0 5. Parabelaehnlicher Graph vom Grad 3.
Funktion 0 Daumen. Erstellen Sie eine Wertetabelle fuer a b d 1 und c -25 und fuegen Sie die 1Ableitung hinzu. Grades durch Substitution loesen im Mathe-Forum fuer Schueler und Studenten Antworten nach dem Prinzip Hilfe zur Selbsthilfe Jetzt Deine Frage im Forum stellen.
Gefragt 9 Aug von neleuwe. Student Student Warum kann man den Verlauf mit einer Funktion 3 grades beschreiben. A Gesucht ist eine ganzrationale Funktion dritten Grades mit dem Tiefpunkt P1-2 deren Wendepunkt im Koordinatenursprung 00 liegt.
Durch 00 -- d0. Bei der Funktion f. Sehen wir uns nun einige Beispiele zu ganzrationale Funktionen an.
Begruende warum es keine ganzrationale Funktion mit folgenden Eigenschaften geben kann. Y 4x 2 2x 6. Der Graph der Funktion schneidet die x-Achse bei x 1 4.
Erlaeutern Sie den Einfluss der Koeffizienten einer ganzrationalen Funktion dritten Grades auf ihren Wendepunkt graphisch mithilfe von GeoGebra. A 1 2. Die Gesamtkosten K eines Betriesbes lassen sich durch eine ganzrationale Funktion 3.
Student Der graph beschreibt uebrigens einen tunnel. Gefragt 13 Okt von Philiprnr. Y 2x 5.
Die zweite Aussage zu der ein Term angegeben werden muss ist die Aussage F ist eine ganzrationale Funktion des dritten Grades und hat genau zwei Nullstellen. Eine ganzrationale Funktion 3.
 Steckbriefaufgabe Funktion 3 Grades Youtube
Steckbriefaufgabe Funktion 3 Grades Youtube
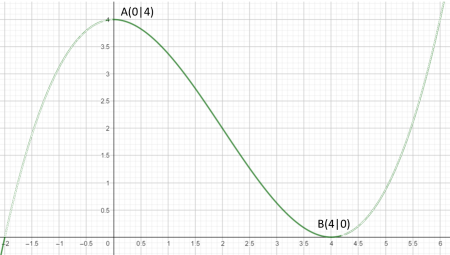 Ganzrationale Funktion 3 Grades Finden Modellieren Mathematik Mathehilfe24
Ganzrationale Funktion 3 Grades Finden Modellieren Mathematik Mathehilfe24
Ganzrationale Funktion 3 Grades Bestimmen
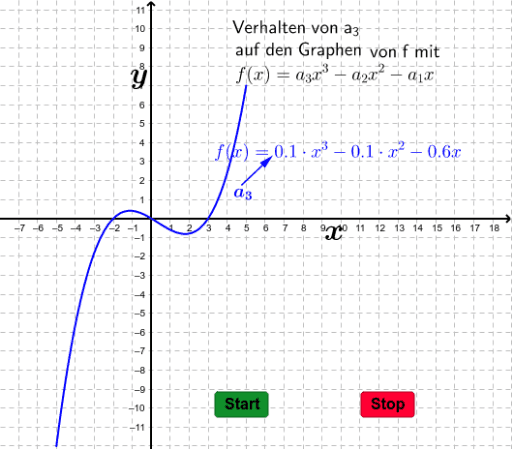 Funktionsverhalten Einer Ganzrationalen Funktion Geogebra
Funktionsverhalten Einer Ganzrationalen Funktion Geogebra
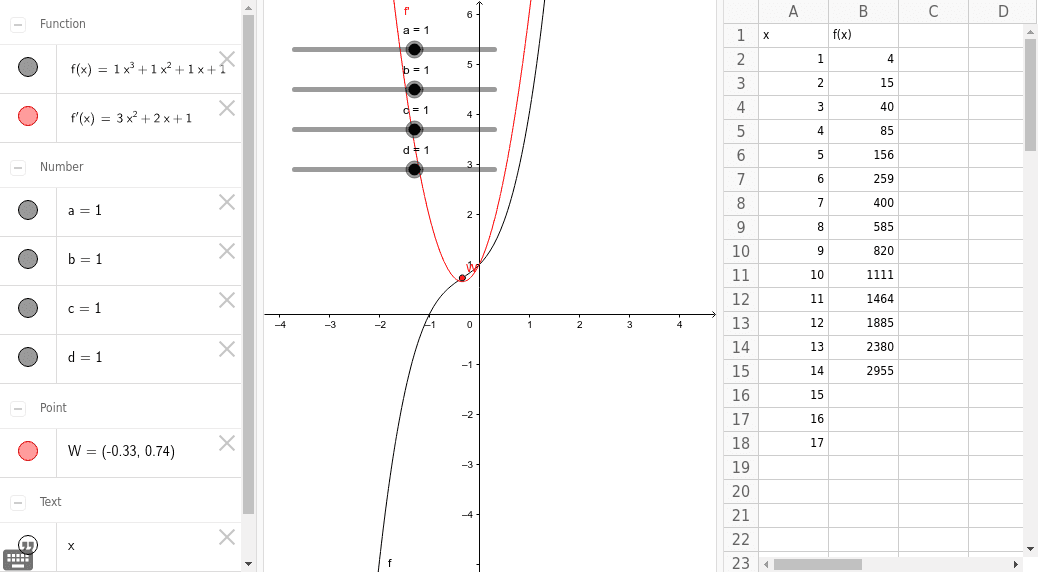 Ganzrationale Funktion 3 Grades Geogebra
Ganzrationale Funktion 3 Grades Geogebra
Graph Einer Ganzrationalen Funktion Dritten Grades Hat In S 1 2 Sattelpunkt Mathelounge
 Ganzrationale Funktionen Ab 3 Grades Youtube
Ganzrationale Funktionen Ab 3 Grades Youtube
 Ganzrationale Funktionen Polynomfunktionen Mit Video
Ganzrationale Funktionen Polynomfunktionen Mit Video
 Nullstellen Berechnen Formeln Beispiele Mit Video
Nullstellen Berechnen Formeln Beispiele Mit Video
Funktionssuche 3 Grades Mathelounge
Ganzrationale Funktion Dritten Grades Aus Tiefpunkt Und Wendepunkt Bestimmen Mathelounge
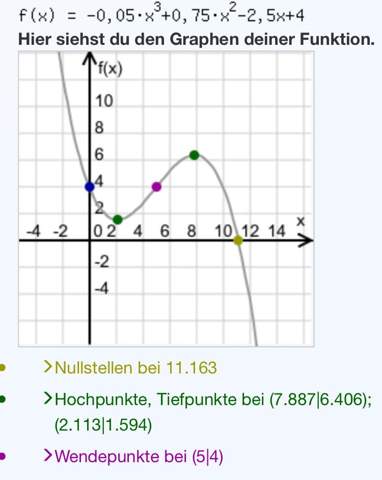 Wie Bekomme Ich Diese Nullstelle 11 16 Funktion 3 Grades Mit Absolutglied Schule Mathematik Deutschland
Wie Bekomme Ich Diese Nullstelle 11 16 Funktion 3 Grades Mit Absolutglied Schule Mathematik Deutschland
 Ganzrationale Funktion Dritten Grades Schule Mathe Mathematik
Ganzrationale Funktion Dritten Grades Schule Mathe Mathematik
Monotonie Von Ganzrationalen Funktionen 3 Grades