Cool Erweiterter Euklidischer Algorithmus Inverse Berechnen

Gesucht ist der grosste gemeinsame Teiler d ggTab von ab dh. Der erweiterte euklidische Algorithmus ist ein Algorithmus aus dem mathematischen Teilgebiet der Zahlentheorie.

Erweiterter Euklidischer Algorithmus Inverse Berechnen - Spaß für meinen eigenen Blog, bei dieser Gelegenheit werde ich Ihnen im Zusammenhang mit erklären Erweiterter Euklidischer Algorithmus Inverse Berechnen. Also, wenn Sie großartige Aufnahmen machen möchten Erweiterter Euklidischer Algorithmus Inverse Berechnen, Klicken Sie einfach auf das Speichersymbol, um das Foto auf Ihrem Computer zu speichern. Sie können heruntergeladen werden. Wenn Sie möchten und möchten, klicken Sie im Beitrag auf "Logo speichern". Der Download erfolgt direkt auf Ihren Heimcomputer.

Erweiterter Euklidischer Algorithmus Inverse Berechnen ist eine wichtige Information, die von Fotos und HD-Bildern begleitet wird, die von allen Websites der Welt stammen. Laden Sie dieses Bild kostenlos in High Definition-Auflösung mit der unten stehenden Option "Download-Schaltfläche" herunter. Wenn Sie nicht die genaue Auflösung finden, nach der Sie suchen, wählen Sie Original oder eine höhere Auflösung. Sie können diese Seite auch einfach speichern, sodass Sie sie jederzeit anzeigen können.

Hier sind Sie auf unserer Website, Artikel oben, veröffentlicht von Babang Tampan. Wir hoffen du mag bleibe hier. Für viele Upgrades und Aktuelle Nachrichten zum folgenden Foto folgen Sie uns bitte auf Twitter, Pfad, Instagram, oder Sie markieren diese Seite auf Lesezeichen Bereich, Wir versuchen Ihnen update regelmäßig mit frisch und neu Grafiken, wie dein Erkunden und finde das Richtige für dich. Heute Wir sind erfreut, zu erklären dass wir gefunden ein extremes interessanter Nische, der hervorgehoben werden soll, einige Leute suchen Einzelheiten von zu finden, und sicher einer von ihnen bist du, nicht wahr?

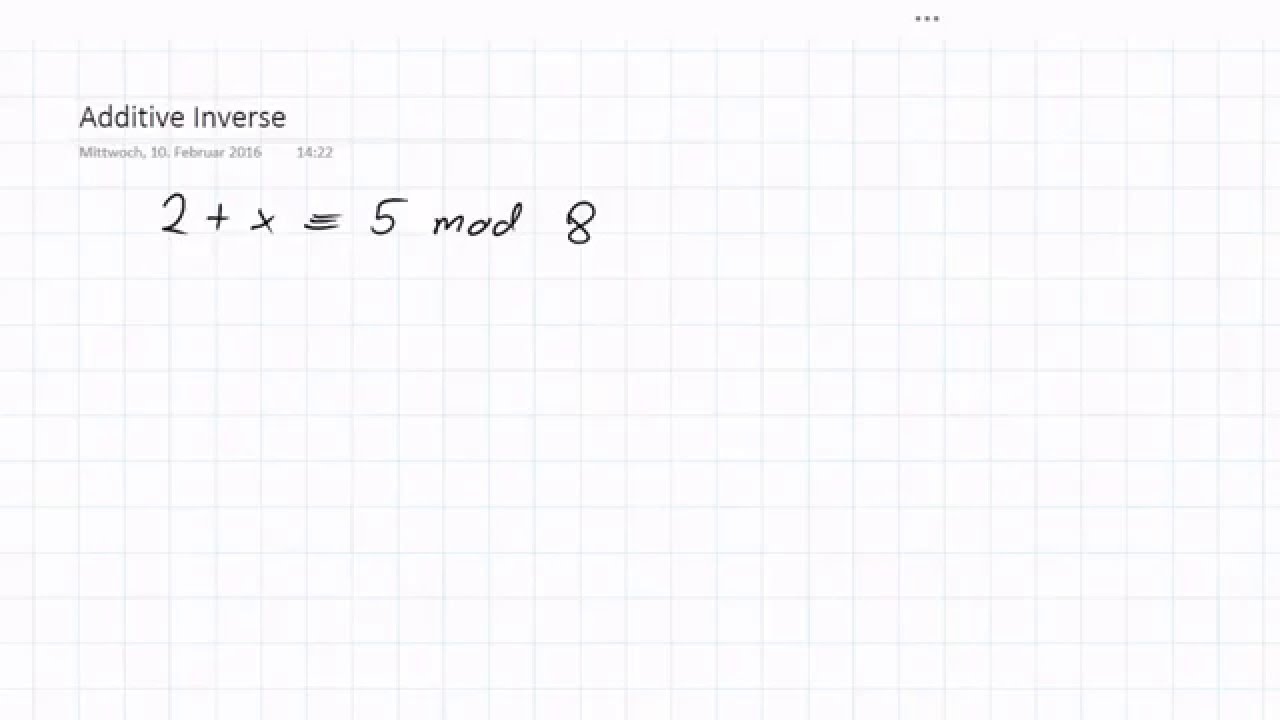Additive Inverse Berechnen Youtube

Jene eindeutig bestimmte positive Zahl b m die die Gleichung.

Erweiterter euklidischer algorithmus inverse berechnen. Der euklidische Algorithmus ist ein Verfahren um den groessten gemeinsamen Teiler zweier positiver ganzer Zahlen zu berechnen. GgT a b displaystyle operatorname ggT ab zweier natuerlicher Zahlen. Mk ist die Division mit Rest die im Schritt k auszufuehren ist.

Dann ist c a 1 mod m das Inverse von a. Dieser Algorithmus laesst sich so erweitern dass hiermit auch modulare Inverse bestimmt werden koennen. Wir betrachten zunaechst ein Beispiel.

Der ggT von 22 und 154 ist 22 letzter Rest im Euklidschen Algorithmus. Eine ganze Zahl d mit foldgenden Eigenschaften. 122 0154 22.

Christian Spannagel an der PH Heidelberg. Uebersicht ueber alle Videos und Materialien unter httpwikiszumdezumPH_Heidelberg. 1 Euklidischer Algorithmus Euklidischer Algorithmus.

Erweiterter euklidischer Algorithmus Der euklidische Algorithmus ist ein Verfahren um den groessten gemeinsamen Teiler zweier positiver ganzer Zahlen zu berechnen. Berechnen und ub erprufen Sie. Alternative Berechnung mit Matrizen.

Nun wird sukzessive rueckwaerts eingesetzt um 22 dh. Dabei werden jeweils nur die zwei letzten Zeilen gespeichert da nur diese fuer die Berechnung der folgende Zeile benoetigt wird. Mithilfe von Matrizen laesst sich als praktisches Verfahren ein erweiterter euklidischer Algorithmus berechnen und darstellen.

Sind a und m zwei teilerfremde positive ganze Zahlen so kann eine erweiterte Version dieses Algorithmus verwendet werden um die Inverse von a modulo m dh. Ein Algor i thmus hat nicht mit dem musikalischen Rhythmus nichts gemein. Die Grundlage dazu bietet die Formel mk nk qk rk.

Das inverse Element eines Elements a n laesst sich mit Hilfe des erweiterten euklidischen Algorithmus berechnen. Erweiterter Euklidischer Algorithmus. Dieser Rechner verwendet den erweiterten euklidischen Algorithmus der neben den groessten gemeinsamen Teiler von den Ganzzahlen a und b auch den Lemma von Bezout Koeffizienten berechnet.

Sind a und m zwei teilerfremde positive ganze Zahlen so kann eine erweiterte Version dieses Algorithmus verwendet werden um die modulare Inverse von a mod m dh. Der Algorithmus wurde bereits ca. Euklidischer Algorithmus und Inverse in ZpZ Seien ab Z.

Der euklidische Algorithmus berechnet den gr oˇten. Jene eindeutig bestimmte positive Zahl b m die die Gleichung. Auf diese Art und Weise lassen sich auch Inverse in der Modulorechnung bestimmen.

Das Verfahren ist nach dem griechischen Mathematiker Euklid benannt der es in seinem Werk Die Elemente beschrieben hat. Die Gleichung wird zu 175 mod 17 und damit ist 7 das Inverse zu 5. Euklidischer Algorithmus a Zahl 1 b Zahl 2 Berechnet den ggTa b und die Bezout-Koeffizienten.

Mit ihm laesst sich der groesste gemeinsame Teiler zweier natuerlicher Zahlen berechnen. Den ggT von 22 und 154 als Linearkombination dieser beiden Zahlen darzustellen. Der euklidische Algorithmus berechnet den groessten gemeinsamen Teiler ggt a b von zwei ganzen Zahlen a und b.

Der euklidische Algorithmus ist ein Algorithmus aus dem mathematischen Teilgebiet der Zahlentheorie. HttpsdiscordggvHzfaPz62H Meine Udemy Kurse im Rabatt. Erweiterter euklidischer Algorithmus Der so genannte erweiterte euklidische Algorithmus oder auch binaerer euklidischer Algorithmus von Josef-Stein ist in der Lage mittels Division durch 2 nebst dem ggT zweier Zahlen auch die Inverse und den Restklassenring zu berechnen.

Sind a und m zwei teilerfremde positive ganze Zahlen so kann eine erweiterte Version dieses Algorithmus verwendet werden um die modulare Inverse von a mod m dh. Jene eindeutig bestimmte positive Zahl b m die die Gleichung. Er berechnet neben dem groessten gemeinsamen Teiler.

Das Haupteinsatzgebiet des erweiterten euklidischen Algorithmus ist die Berechnung der inversen Elemente in ganzzahligen Restklassenringen denn wenn der Algorithmus das Tripel ermittelt ist entweder und damit also das multiplikative Inverse von modulo oder aber was bedeutet dass modulo kein Inverses hat. Die Bezout-Koeffizienten s und t der Zahlen n und m erfuellen folgende Beziehung. Erweiterter euklidischer Algorithmus Der euklidischer Algorithmus ist ein Standardalgorithmus zur Berechnung des groessten gemeinsamen Teilers kurz ggT von zwei vorgegebenen natuerlichen Zahlen.

Die Bildung eines Spaltenvektors aus m und n fuehrt zu einer Darstellung mit Uebergangs-Matrix. Damit ergibt sich die Inverse modulo 17. Der erweiterte euklidische Algorithmus berechnet zusaetzlich noch eine Darstellung von ggt a b als ganzzahlige Linearkombination von a und b.

Das so genannte additive Inverse von 8 ist zB. Der erweiterte euklidische Algorithmus ist ein Algorithmus der den groessten gemeinsamen Teiler von zwei Zahlen bestimmt den ggT und zusaetzlich die sogenannten Bezout-Koeffizienten fuer diese zwei Zahlen sehr effizient berechnen kann. Ab mod m1 erfuellt zu berechnen.

Eine andere Moeglichkeit besteht darin das inverse Element durch modulare Exponentiation auf Grundlage des Satzes von Euler zu berechnen. 15 1 5 mod 24 26 1 31 mod 37 38 1 27 mod 43 2.

Erweiterter Euklidischer Algorithmus Ggt Linearkombination Youtube